API Design
The API of matrices is object-oriented and relatively small. It has been designed to be easy to use and still perform well. The Matrix API is quite similar to JAMA, although there are some important differences.- Matrix is an interface definition, not a base class.
- Matrix instances are immutable.
- Parallel algorithms are used to utilize modern CPU architectures.
- API is compatible with Java Operator Overloading.
- Matrix uses heterogeneous data storage implementations.
- Designed for Java 8
- Optional native acceleration
A small number of fixed-dimension matrices are available as classes. These include 2D and 3D affine matrices and rotation matrices. These special purpose matrices are provided as they are often required in 2D/3D applications and require optimal performance and type safety.
Having a Matrix interface instead of an abstract base class allows for more design options when integrating with other (matrix) libraries. It also may take advantage of future Java features such as value-types, which currently seem to exclude class hierarchies, but allow interfaces.
 |
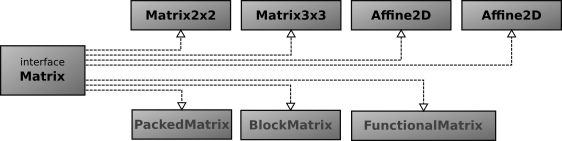| Matrix interface, public and package private implementations |
General Matrix Implementation
General matrices are constructed using static methods on the Matrix interface. These methods will return a matrix implementation suitable for the specified data. The matrices returned by these methods are generally not part of the public API, but package private classes. The type of the returned matrix is chosen based on the specified dimensions of the matrix. There are three categories of matrices.Small Matrices
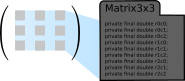Small matrices are matrices with dimensions up to 5x5. Small matrices have generated classes for each possible dimension (Matrix1x1, Matrix1x2, etc). At this scale there are some significant advantages of having generated classes:- Elements are stored as individual instance variables instead of in arrays.
- No dereferences required for accessing element values.
- No bounds checking on indices.
- Better locality for data.
- Less data used.
- Better compiler optimizations available for (final) instance variables.
- Operations are implemented in generated code
- No loops
- No index calculations performed as all elements are available as fields.
- No dimension checks required for generated classes as type system already provides the guarantees.
- Algorithm optimizations possible when dimensions are known in advance.
Currently having all matrices up to 5x5 generated seems to be a good balance as this includes some matrix dimensions that are very common indeed. The matrix implementations Matrix2x2 and Matrix3x3 are examples of such often used matrices. These matrices are part of the public API, in contrast to the other generated matrices.
Medium Matrices
The element values are stored in either a row-major (as shown in the illustration) or column-major packed array. This means that transposing a matrix does not involve any operations on the stored elements, just a different ordering state. Other operations can generally efficiently operate on both row-orderings, which means that transposing a matrix does not involve much (or any) overhead.
Using a packed array for data storage is limited mostly by data locality. For instance in a row-major packed array, elements in a single column are not stored together in memory.
Large Matrices
Operations such as addition, subtraction, multiplication and scaling are implemented using parallel algorithms, speeding up the execution on multi-core and multi-processor systems.
If a sub-matrix is known to only contain zero values, it will not store this data. Basic operations will take advantage of this knowledge and perform considerably better.
There is currently no specific support for band or sparse matrices. These matrices may, however, take some advantage of the empty sub-matrix optimizations.
Functional Matrix
A special type of matrix is provided to allow functional style definition of a matrix. A single lambda function defines the element data of the matrix, which is a very flexible way of constructing a matrix. Basic operations will result in new functional matrices, providing lazy evaluation without intermediate data storage. For example, an 100x100 identity matrix can be created using the following instruction:Matrix.function(100,100, (row,column)-> row == column ? 1 : 0);
Low-level API and Native Accelerators
The low-level API provides support for some matrix operations. It can be used to optimize performance critical algorithms that can benefit from this low-level code. The low-level API operates on packed byte arrays.The low-level API has been designed to be replaced by a native implementation. Using a native accelerator, some operations (i.e. matrix multiplication) can be accelerated considerably. As the low-level API is used by Matrix implementations, using an native accelerator will also boost their performance.
A native accelerator has been implemented for Intel x64 processors using OpenBLAS.
MATLAB/Octave
Matrices can be constructed from a text string. The format is similar and compatible with the format used in MATLAB/Octave. This means you can construct a matrix like this:Matrix.valueOf("1,2;3,4");
The string representation of a matrix is similar to MATLAB/Octave and can also be used to create a matrix from a text string. This means that matrix input and output can be copied from MATLAB/Octave to Java code.
This is particularly useful when porting code and creating unit tests.
Links
- Thorwin Math
- Java Matrix Package (JAMA)
- Java Operator Overloading (Java-OO)
No comments:
Post a Comment